San Diego, 07 de Junio de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas
Tema: Operaciones con unidades de tiempo
Conversión entre unidades de tiempoPara convertir una unidad de tiempo a otra, multiplicamos o dividimos de acuerdo al planteamiento. Si vamos a convertir de una medida mayor a una menor debemos multiplicar.
Por ejemplo, si vamos a convertir 3 horas a segundos, debemos multiplicar porque está expresado en una medida mayor a una menor, pero en este caso debemos hacer dos multiplicaciones, ya que antes de llevar esas 3 horas a segundos debemos llevarlas primero a minutos.
Recuerden que en la clase anterior aprendimos las equivalencias de las medidas; entonces dado que a hora tiene 60 minutos, vamos a multiplicar 3 horas x 60 minutos, obteniendo como resultado 180 minutos. Finalmente debemos llevar el resultado obtenido a segundos, y en ese caso multiplicamos ahora 180 minutos x 60 segundos, que es igual a 10800.
Así pues, 3 horas equivalen a 10800 segundos.
En otro caso, si deseamos convertir 72 horas a días, debemos dividir porque esta expresado en un tiempo menor a uno mayor, entonces vamos a dividir 72 horas en lo que equivale el día que son 24 horas, obteniendo como resultado 3 días.
Así pues, en 72 horas hay 3 días.
Otros ejemplos:
a) 40 años a décadas
40 ÷ 10= 4
R= En 40 años hay 4 décadas.
---------------
b) 5 años a días
5 x 365 = 1825
R= En 5 años hay 1825 días
--------------
c) ¿Cuántos años hay en en 2 milenios, 5 siglos y 3 lustros?
2 x 1000 = 2000
5 x 100 = 500
3 x 5 = 15
R= En 2 milenios, 5 siglos y 3 lustros hay 2515 años.
ACTIVIDADES
Realiza las siguientes conversiones
- 525 años a lustros
- 11 horas a minutos
- 850 años a décadas
- 729 minutos a horas
- 8600 segundos a minutos
- 12 años a meses
- 5 horas a segundos
- 7200 años a siglos
- 96 años a meses
Responde los planteamientos
- ¿Cuántos años hay en 2 siglos y 3 décadas?
- ¿Cuántas semanas hay en 10 meses?
- ¿Cuántos años hay en 3 milenios, 5 siglos y 6 décadas?
- ¿Cuántos quinquenios hay en 40 años?
- ¿Cuántos meses hay en 5 lustros?
San Diego, 06 de Junio de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas
Tema: Unidades de tiempo
El tiempo lo podemos medir con instrumentos como el reloj y los calendarios a partir de acontecimientos. Las unidades de medidas de tiempo varían de acuerdo con el instrumento que utilicemos.
Las unidades de tiempo pueden ser:
- Menores o iguales que un día: segundos, minutos, horas y días.
- Menores que un año: días, semanas y meses.
- Mayores que un año: bienio, quinquenios o lustro, décadas, siglos y milenios.
ACTIVIDAD
1) Señala la equivalencia de cada unidad de tiempo
- El día equivale a _____ horas
- La hora equivale a _____minutos
- El minuto equivale a ____ segundos
- La semana equivale a ____ días
- El mes equivale a _______ semanas
- El mes equivale a ____________ días
- Un trimestre equivale a ____ meses
- Un semestre equivale a _____ meses
- El año equivale a _____ días
- El año equivale a _____ meses
- El año equivale a _____ trimestres
- El año equivale a _____ semestre
- El quinquenio o lustro que equivale a _____ años
- La década que equivale a _____ años
- El siglo que equivale a ______ años
- El milenio que equivale a _____ años
El tiempo lo podemos medir con instrumentos como el reloj y los calendarios a partir de acontecimientos. Las unidades de medidas de tiempo varían de acuerdo con el instrumento que utilicemos.
Las unidades de tiempo pueden ser:
- Menores o iguales que un día: segundos, minutos, horas y días.
- Menores que un año: días, semanas y meses.
- Mayores que un año: bienio, quinquenios o lustro, décadas, siglos y milenios.
ACTIVIDAD
1) Señala la equivalencia de cada unidad de tiempo
- El día equivale a _____ horas
- La hora equivale a _____minutos
- El minuto equivale a ____ segundos
- La semana equivale a ____ días
- El mes equivale a _______ semanas
- El mes equivale a ____________ días
- Un trimestre equivale a ____ meses
- Un semestre equivale a _____ meses
- El año equivale a _____ días
- El año equivale a _____ meses
- El año equivale a _____ trimestres
- El año equivale a _____ semestre
- El quinquenio o lustro que equivale a _____ años
- La década que equivale a _____ años
- El siglo que equivale a ______ años
- El milenio que equivale a _____ años
San Diego, 21 de Mayo de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas
Tema:
PROBLEMAS APLICANDO EL PORCENTAJE
Para resolver problemas con porcentaje, recuerden que lo primero que debemos hacer es identificar el elemento que voy a calcular, este puede ser alguna cantidad o algún porcentaje, el elemento que calculemos será sustituido por la variable x. Luego de ello aplicamos una regla de tres.
Cantidad inicial______________ Cantidad relacionada con el porcentaje
100 _______________ X
Ejemplos:
Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?
De los 684 lanzamientos que realizó Alberto, falló 513. ¿Qué porcentaje de lanzamientos fallidos tiene Alberto?
ACTIVIDAD
Resuelve los siguientes planteamientos:
- En un examen han aprobado 3 alumnos de un clase de 30, ¿qué porcentaje representan?
- Al comprar un monitor que cuesta 450 Bs nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar?
- Un jugador de baloncesto ha encestado 8 tiros libres de un total de 15, ¿qué porcentaje representan?
- Se vende un artículo con una ganancia del 15% sobre el precio de costo. Si se ha comprado en 80 Bs. Halla el precio de venta.
PROBLEMAS APLICANDO EL PORCENTAJE
|
|
Para resolver problemas con porcentaje, recuerden que lo primero que debemos hacer es identificar el elemento que voy a calcular, este puede ser alguna cantidad o algún porcentaje, el elemento que calculemos será sustituido por la variable x. Luego de ello aplicamos una regla de tres.
Cantidad inicial______________ Cantidad relacionada con el porcentaje
100 _______________ X
Ejemplos:
Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?
De los 684 lanzamientos que realizó Alberto, falló 513. ¿Qué porcentaje de lanzamientos fallidos tiene Alberto?
ACTIVIDAD
Resuelve los siguientes planteamientos:
- En un examen han aprobado 3 alumnos de un clase de 30, ¿qué porcentaje representan?
- Al comprar un monitor que cuesta 450 Bs nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar?
- Un jugador de baloncesto ha encestado 8 tiros libres de un total de 15, ¿qué porcentaje representan?
- Se vende un artículo con una ganancia del 15% sobre el precio de costo. Si se ha comprado en 80 Bs. Halla el precio de venta.
San Diego, 17 Mayo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: El Porcentaje
Es una relación de proporción donde se comparan dos cantidades, a partir de razones basadas en 100 unidades. El porcentaje se indica con el signo % (tanto por ciento) y en general, el porcentaje es una cantidad que se suma o se resta de la cantidad original.
Para calcular el porcentaje de un x% de un número n, se multiplica el tanto por ciento x por n, y el producto se divide entre 100.
Para calcular el porcentaje que representa una cantidad de otra, se aplica la regla de tres.
Pulsa aquí para ver otra forma de resolver ejercicios con porcentajes.
Es una relación de proporción donde se comparan dos cantidades, a partir de razones basadas en 100 unidades. El porcentaje se indica con el signo % (tanto por ciento) y en general, el porcentaje es una cantidad que se suma o se resta de la cantidad original.
Para calcular el porcentaje de un x% de un número n, se multiplica el tanto por ciento x por n, y el producto se divide entre 100.
Para calcular el porcentaje que representa una cantidad de otra, se aplica la regla de tres.
Pulsa aquí para ver otra forma de resolver ejercicios con porcentajes.
ACTIVIDAD
1) Resuelve hallando el valor que representa el porcentaje.(Como en el primer ejemplo, con su procedimiento)
2) Resuelve hallando el porcentaje que representa en cada caso (Como en el segundo ejemplo, con su procedimiento).
125..........50030..............60100........100080............400
San Diego, 22 Mayo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Resolución de problemas aplicando la Regla de Tres
Para resolver un problema aplicando la regla de tres, primero leemos el planteamiento, luego extraemos los datos, como se detalla en la clase anterior, y finalmente aplicamos la regla de tres directa o inversa según sea el caso.
Veamos a través de un vídeo un ejemplo de ello.
Pulsa también aquí para ver el vídeo
ACTIVIDADES
1) Aplica la regla de tres que corresponde (directa o inversa) en cada planteamiento.
- Ana tiene 10 costureras que la ayudan a hacer cortinas para hogares. Si entre las 10 se tardan 30 días. ¿Cuánto se tardarían con la ayuda de 15 costureras más?
-
- Alejandra es ingeniera y tiene a su cargo la construcción de un edificio. Si para construir 6 niveles del necesitó 1200 remaches, ¿Cuántos remaches utilizaría en 8 niveles?
- Necesito 5 huevos para preparar una torta. ¿Cuántos necesitaré para preparar 12 tortas?
- El atún es un pez que vive en mares tropicales y templados. Si un atún nada 30 km en una hora. ¿Cuántos kilómetros nadará en 5 horas?
- Para la venta de 5 kg de naranjas, Leonardo se ganó Bs. 20. ¿Cuántos bolívares ganará si vende 25 kg de naranjas?
- Ana tiene 10 costureras que la ayudan a hacer cortinas para hogares. Si entre las 10 se tardan 30 días. ¿Cuánto se tardarían con la ayuda de 15 costureras más?
- Alejandra es ingeniera y tiene a su cargo la construcción de un edificio. Si para construir 6 niveles del necesitó 1200 remaches, ¿Cuántos remaches utilizaría en 8 niveles?
- Necesito 5 huevos para preparar una torta. ¿Cuántos necesitaré para preparar 12 tortas?
- El atún es un pez que vive en mares tropicales y templados. Si un atún nada 30 km en una hora. ¿Cuántos kilómetros nadará en 5 horas?
- Para la venta de 5 kg de naranjas, Leonardo se ganó Bs. 20. ¿Cuántos bolívares ganará si vende 25 kg de naranjas?
San Diego, 17 Mayo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Regla de Tres
Una regla de tres es directa si sus magnitudes son directamente proporcionales. Una regla de tres es inversa si sus magnitudes son inversamente proporcionales.
Observa cómo se resuelven los siguientes problemas, aplicando la regla de tres.
a) Tres libros iguales tienen 360 páginas ¿cuántas páginas habrá en 8 libros iguales?
Las magnitudes número de libros y número de página son directamente proporcionales, por lo tanto, la regla de tres que se utilizará es directa.
b) En un campamento de 10 niños, hay alimento para 30 días. Si llegan 5 niños más, ¿cuántos días durarán los alimentos?
Las magnitudes número de niños y número de días que duran los alimentos son inversamente proporcionales, por lo tanto, la regla de tres que se utiliza es inversa.
Pulsa aquí para ver cómo se resuelve la regla de tres directa e inversa.
ACTIVIDAD
Hallar el valor del término desconocido, aplicando la igualdad de productos cruzados en una proporción.
San Diego, 09 Mayo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Resolución de una Ecuación y método de sustitución o comprobación.
El método de sustitución es una manera de resolver sistemas de ecuaciones. Para usar el método de sustitución, toma una ecuación y encuentra una expresión para una de las variables en términos de la otra variable. Luego sustituye esa expresión por la variable en la segunda ecuación.
- Se despeja una incógnita de las ecuaciones.
- Se resuelve la ecuación.
- El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.
Ejemplo
ACTIVIDAD
1 Hallar el valor de la incógnita y aplicar el método de sustitución.
5x - 5 = 25
8 8 - 4x = 44
b) 60 + 4x - 20 = 52
c) 16 + Y = 23
d) 30x- 7 = 35
e) 40 = 76 - Y
f) 8x = 56 - 16
San Diego, 03 Mayo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Resolución de problemas a través de una Ecuación.
Para representar un problema mediante una ecuación, le asignamos a la incógnita del problema una letra que será la incógnita de la ecuación. Por ejemplo, veamos el siguiente problema:
El triple de la edad de José es igual a treinta y seis. ¿Cuántos años tiene José?
Para resolverlo hacemos lo siguiente:
1. Le asignamos la letra a la incógnita del problema (Como la edad de José es lo que queremos conocer, entonces ésa es nuestra incógnita y le asignamos la letra “j”).
2. Leemos la situación y cada palabra la transformamos y sustituimos por un símbolo matemático, de esta manera planteamos la ecuación que refleja la situación.
Finalmente la ecuación es 3j = 36
PASOS PARA RESOLVER UN PROBLEMA
1. Leer el problema
2. Extraer los datos
3. Identificar la operación
4. Resolver la operación
5. Responder el problema
6. Comprobar el resultado.
EJEMPLO DE CÓMO RESOLVER UN PROBLEMA UTILIZANDO LA ECUACIÓN
El doble de la edad de María, disminuida dos años es igual a veinticuatro años. ¿Cuál es la edad de María?
Para resolverlo, primero identificamos los datos. (La edad de María es la incógnita por esos le asignamos la letra m. Es decir, “m” representa la edad de María).
Luego, planteamos la operación. En este caso es una ecuación.
2m – 2 = 24
Resolvemos la ecuación:
2 m – 2 = 24
2 m + 2 - 2 = 24 + 2
2m = 26
2m = 26
2 2
m = 13
También la podemos resolver como se explico en la clase de whasapp del viernes 16/04/2021
2 m – 2 = 24
2 m = 24 + 2
2m = 26
m = 26
2
m = 13
Importante, cuando dice disminuidos restamos, cuando dice aumentamos sumamos.
ACTIVIDADES
1. Resuelvo los siguientes problemas.
a) Un número aumentado en tres unidades es igual a catorce. ¿Cuál es el número?
b) La edad de Carmen aumentada cuatro años es igual a diecinueve disminuidos tres años. ¿Cuál es la edad de Carmen?
c) Un número aumentado cinco unidades es igual a quince unidades disminuidas en seis unidades. ¿Cuál es el número?
d) La edad de Antonio aumentada en cuatro unidades, más la edad de su hermana suman 20. Si la hermana de Antonio tiene 6 años, ¿Cuál es la edad de Antonio?
San Diego, 26 Abril de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Resolución de una Ecuación
La solución de una ecuación es el valor de la incógnita con el cual se cumple la igualdad. Por ejemplo, la ecuación x+ 9 = 15 tienen como solución x= 6, porque es el número que satisface la igualdad 6 + 9 = 15
Para hallar la solución de una ecuación construimos ecuaciones equivalentes a la ecuación dada. Para ello observamos cómo es la ecuación, ella puede tener una de estas formas básicas.
· Ecuación con incógnita simple, donde la incógnita no está multiplicada por ningún número.
Por ejemplo: x + 4 = 12
· Ecuaciones con incógnita multiplicada por un coeficiente. Llamamos coeficiente a los números que multiplican la variable.
6x + 4 = 16
Solución de una ecuación incógnita simple
Para hallar la solución de una ecuación con incógnita simple, por ejemplo, la solución de x – 8 = 15, hacemos lo siguiente:
1. Eliminamos la constate que suma o resta, restando o sumando a ambos lados de la igualdad el mismo número de la constante que acompaña a la variable. En este caso sumamos 8.
X + 8 – 8 = 15 + 8
2. Efectuamos la suma o la resta necesaria.
X + 0 = 23
X = 23
Finalmente, la solución de la ecuación es x = 23.
Solución de una ecuación con variable multiplicada por un coeficiente.
Para hallar la solución de una ecuación con variable multiplicada por un coeficiente, por ejemplo, la solución de 3p + 2 = 20, hacemos lo siguiente:
1. Eliminamos la constante que suma o resta, restando o sumando a ambos lados de la igualdad el mismo número de la constante que acompaña a la variable. En este caso restamos 2 en ambos miembros.
3p + 2 – 2 = 20 - 2
2. Efectuamos las sumas o las restas necesarias.
3p + 0 = 18
3p = 18
3. Dejamos la incógnita sola dividiendo ambos lados de la igualdad entre el mismo número del coeficiente que multiplica a la incógnita.
3p = 18
3 3
P = 6
Finalmente la solución de la ecuación es p = 6
ACTIVIDAD
1 Hallar el valor de la incógnita
a) 2x + 12 = 24
b) 7 + 2x = 19
c) 2 + x = 18
d) 3x- 3 = 24
e) 7x – 21 = 28
f) 4x = 56
g) 1 +6x = 37
h) 8x – 3 = 13
i) X – 4 = 10
San Diego, 25 Abril de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Las Ecuaciones
ECUACIONES
Ecuación | Incógnita | Constantes | Primer miembro | Segundo miembro |
3 x + 9 = 15 | x | 9 y 15 | 3x + 9 | 15 |
3 = 10 –x |
|
|
|
|
Y + 4 + 1 = 12 |
|
|
|
|
2 w – 5= 6 + 5 |
|
|
|
|
b) 16 + 4 = 20 ____
c) x - 12 = 5 ____
d) 5x + 3 = 8 ____
e) 12 - 1 = 11 ____
f) 5 + 3x = 14 ____
g) 5x + 7 = 27 ____
19 - 3 = 16 ____
San Diego, 20 Abril de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Operaciones combinadas con fracciones. (Repaso)
ACTIVIDAD
1) Resuelve las operaciones combinadas de fracciones:
San Diego, 18 Abril de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Operaciones combinadas con fracciones.
Actividades
1) Copiar el tema del libro.
2) Resolver
San Diego, 24 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: División y simplificación fracciones.
FRACCIÓN INVERSA
La fracción inversa de una fracción es aquella que tiene un numerador y el denominador invertido con respecto a la fracción dada.
El producto de una fracción por su inversa siempre es igual a la unidad.
Ejemplo:
DIVISIÓN DE FRACCIONES
Para dividir fracciones sin hallar fracción inversa multiplicamos de forma cruzada numeradores por denominadores.
Veamos los siguientes ejemplos:
SIMPLIFICACIÓN DE FRACCIONES
La simplificación de una fracción consiste en transformarla en una fracción equivalente más simple. En la simplificación de fracciones se divide el numerador y denominador por un mismo número. Se empieza a simplificar probando por los primeros. números primos: 2, 3, 5, 7…
Ejemplos:
ACTIVIDADES 1) Investigar la división de fracciones con un número natural, con dos ejemplos.
2) Realiza las siguientes divisiones, luego simplifica hasta obtener una fracción irreducible.
3) Resuelve cada problema.
FRACCIÓN INVERSA
La fracción inversa de una fracción es aquella que tiene un numerador y el denominador invertido con respecto a la fracción dada.
El producto de una fracción por su inversa siempre es igual a la unidad.
Ejemplo:
DIVISIÓN DE FRACCIONES
Para dividir fracciones sin hallar fracción inversa multiplicamos de forma cruzada numeradores por denominadores.
Veamos los siguientes ejemplos:
SIMPLIFICACIÓN DE FRACCIONES
La simplificación de una fracción consiste en transformarla en una fracción equivalente más simple. En la simplificación de fracciones se divide el numerador y denominador por un mismo número. Se empieza a simplificar probando por los primeros. números primos: 2, 3, 5, 7…
Ejemplos:
3) Resuelve cada problema.
San Diego, 21 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Propiedades de la Multiplicación con fracciones.
En la multiplicación con fracciones se cumplen las propiedades conmutativas, asociativa y elemento neutro.
La propiedad conmutativa indica que a cambiar el orden de los factores el resultado no se altera. Por ejemplo.
ACTIVIDAD
1) Resuelve y escribe el nombre de la propiedad aplicada.
San Diego, 16 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Multiplicación de fracciones.
El producto de dos o más fracciones es otra fracción que tiene como numerador el producto de los numeradores, y como denominador el producto de los denominadores.
1) En este caso multiplicamos numerador con numerador y el resultado lo colocamos en el numerador de la fracción resultante.
2) Multiplicamos denominador con denominador y el resultado lo colocamos en el denominador de la fracción resultante. Ejemplos.
E
ACTIVIDAD
1) Resuelve aplicando la multiplicación de fracciones
San Diego, 14 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Suma y resta de fracciones. (Repaso)
San Diego, 10 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Suma y resta de fracciones.
ACTIVIDADES
San Diego, 07 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Orden de fracciones (Repaso).
ACTIVIDAD
San Diego, 03 de Marzo de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: Orden de fracciones.
Para ordenar dos o más fracciones utilizamos las relaciones de orden "mayor que" (≥), "menor que" (≤) o "igual a" (=). Para ello, observamos sus numeradores y denominadores y escogemos uno de los siguientes criterios:
Pulsa aquí para ampliar el contenido.
ACTIVIDADES
San Diego, 22 de Febrero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemática.
Tema: El m.c.m y m.c.d (repaso).
ACTIVIDADES
Hallar el m.c.m y m.c.d de:
- 12, 26 y 42
- 35 y 14
- 10, 30 y 50
- 4, 8 y 14
- 36 y 6
San Diego, 17 de Febrero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: El máximo común divisor (m.c.d).
El máximo común divisor (m.c.d.) de dos o más números es el mayor de los divisores que tienen en común dichos números.
El m.c.d. nos permite resolver algunos problemas. Por ejemplo, para cortar listones de madera de 8 cm y 12 cm, en listones más pequeños del mismo tamaño sin que sobre ninguno, hacemos lo siguiente:
San Diego, 15 de Febrero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: El mínimo común múltiplo (Repaso).
ACTIVIDADES
1) Calcula el m.c.m. Para ello recuerda que debes descomponer en factores primos.
- 8,14 y 20
- 12 y 18
Resuelve: 1)Luis y María practican deportes en el paseo Los Próceres. Luis recorrió el lugar en 45 minutos; María en 35 minutos. Si parten juntos, y durante todo el día le dan la vuelta a ese sitio, ¿Cuánto tiempo debe transcurrir para encontrarse de nuevo?
San Diego, 07 de Febrero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: El mínimo común múltiplo.
Mínimo común múltiplo
El mínimo común múltiplo (m.c.m) de dos o más números es el menor de los múltiplos comunes (distintos a cero) de dichos números.
Para calcular el m.c.m. descomponemos los números en sus factores primos. Por ejemplo, podemos calcular en cuanto tiempo coincidirán Javier, Pedro y Andrés en el campo de fútbol si Javier asiste cada 6 días, Pedro asiste cada 12 días y Andrés cada 30 días. Para ello, se hace lo siguiente:
1. Descomponemos en factores primos cada número.
2. Seleccionamos de da factores comunes y no comunes con su mayor exponente. En el siguiente caso sería 22, 3 y 5.
3. Multiplicamos los factores seleccionados: 22,x 3 x 5= 4 x 3 x 5= 604. Entonces, Javier, Pedro y Andrés se encontrarán cada 60 días.
Veamos otro ejemplo:
ACTIVIDAD
1) Calcula el m.c.m. Para ello recuerda que debes descomponer en factores primos.
- 27 y 81
- 24 y 10
- 64 y 40
- 18, 12 y 20
- 8, 14 y 18
San Diego, 04 de Febrero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Número primos y números compuestos.
Los números primos son aquellos números que sólo tienen dos divisores exactos, el número 1 y el número que se divide. Por ejemplo, los números 3, 5, 11, 29, 37 y 43 son números primos porque sólo tienen dos divisores: el 1 y el mismo número.
En el siguiente cuadro podemos observar los números primos del 1 al 100, representados con el color rosa. El grupo de números de color azul pertenecen a los números compuestos
Los números compuestos son aquellos números que tienen más de dos divisores exactos; es decir, que además de ser divisibles por el número 1 y por ellos mismos también son divisibles por otros números. Por ejemplo, los números 4, 6, 16, 24 y 35 son números compuestos porque tiene varios divisores, además del 1 y el mismo número.
Pulsa aquí para ampliar el contenido
Pulsa aquí
ACTIVIDAD
Del siguiente grupo de números determinar los que son primos y los que son compuestos, hallando sus divisores:
- 48
- 31
- 86
- 64
- 23
- 11
- 7
- 99
- 36
- 21
- 49
- 27
San Diego, 31 de Enero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Múltiplos y divisores
Los números que se puede escribir como el producto de dos o más factores son divisibles por cada uno de dichos factores.
Así mismo, los números que se pueden escribir como el producto de dos o más factores son múltiplos de cada uno de dichos factores.
Los múltiplos (M) de un número son todos aquellos que resulta de multiplicar ese número por otro número cualquiera. Los múltiplos de un número son infinitos. Un número es múltiplo de sí mismo y el cero es múltiplo de cualquier número.
Por ejemplo, los múltiplos del número 5 pueden ser:
5x0=0; 5x1=5; 5x2=10; 5x3=15; 5x4=20; 5x5=25...
Algunos múltiplos del número 5 son: M(5) = 0; 5; 10; 15; 20; 25;...
Un número es divisible entre otros número cuando el resultado de la división es exacto, es decir, el residuo es cero (0). Por ejemplo, el número 28 es divisible exactamente entre 1, 2, 4,7 y 28.
28/1=28; 28/2=14; 28/4=7; 28/7=4; 28/28=1
Por lo tanto, los divisores del número 28 son: 1,2,4, 7 y 28.
Criterios de divisibilidad
Los criterios de divisibilidad son reglas que nos permiten determinar si un número es divisible entre otro. Veamos algunos de esos criterios.
- Un número es divisible entre 2 cuando se última cifra es par. Por ejemplo, 50, 28 y 76 son divisibles entre dos. Pero 17 no lo es porque 7 es impar.
- Un número es divisible entre 3 cuando la suma de sus cifras es múltiplo de 3. Por ejemplo, 423 es divisible entre 3 porque 4 + 2 + 3 = 9 y 9 es múltiplo de 3. Pero 29 no lo es porque 2 + 9 = 11
- Un número es divisible entre 5 cuando su última cifra es cinco o cero. Por ejemplo, 500, 255 y 20 son divisibles entre 5. Pero 36 no lo es porque termina en 6.
ACTIVIDADES
a) 4
b) 10
San Diego, 24 de Enero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Propiedades de la adición y la multiplicación (Ejercicios)
Resuelve e identifica cada propiedad de la adición y la
multiplicación.
- (3,2 + 3) x 2 + 0=
- (15,2 x 3) +2 x 1 =
- (28 + 3) +2=
- (15000 x 2) x 1 =
- 3,4 x (3 + 2 + 1) =
San Diego, 19 de Enero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Propiedades de la adición y la multiplicación
En la adición y en la multiplicación se cumplen las propiedades: conmutativa, asociativa y elemento neutro. También existe la propiedad distributiva de la multiplicación con respecto a la adición.Esta última se aplica cuando uno de los factores es una suma o resta con dos o más elementos, y consiste en multiplicar cada uno por el factor que se encuentra fuera del paréntesis y luego sumar o restar los productos.
Propiedad Conmutativa
Adición: el orden de los factores no altera la suma
Multiplicación: el orden de los factores no altera el producto.
Propiedad Asociativa
Adición: Se obtiene el mismo resultado agrupando de diferentes formas.
Multiplicación: al agrupar de distintas formas entre paréntesis, obtenemos el mismo resultado.
Adición: al sumar cero a un número, se obtienen el mismo número.
Propiedad Distributiva
Para multiplicar una suma por un número, se multiplica cada sumando por el número. Luego se suman los productos obtenidos.
Pulsa aquí para ver a detalle los ejemplos de las propiedades de la Adición.
Pulsa aquí para ver a detalle los ejemplos de las propiedades de la Multiplicación
Para multiplicar una suma por un número, se multiplica cada sumando por el número. Luego se suman los productos obtenidos.
Pulsa aquí para ver a detalle los ejemplos de las propiedades de la Adición.
Pulsa aquí para ver a detalle los ejemplos de las propiedades de la Multiplicación
ACTIVIDADES
Resuelve e identifica cada propiedad:
- (238,9 + 4,7) + 79,9 =
- (324 x 1,2) x 6,2 =
- 6 x (23,7 + 15,9) =
- 6241 + 0 =
- 321 x 4,5 =
- 1241,1 x 1 =
San Diego, 13 de Enero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: La potenciación. (Continuación)
Operaciones combinadas con potencias
Para realizar operaciones combinas con potenciación,
resolvemos primeros las potencias, luego las multiplicaciones o divisiones, y
por último las adiciones y sustracciones.
Ejemplo:
Actividades
1. Resuelve las siguientes potencias
2. Resuelve las operaciones combinadas con potencias
3. Completa el cuadro según el ejemplo
San Diego, 10 de Enero de 2022
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: La potenciación.
La potenciación es la manera de efectuar el producto de factores iguales. Los términos de una potenciación son: la base, que es el factor que se repite; y el exponente, que indica el número de veces que se repite el factor.
La anterior potencia se lee tres elevado a la cuatro
Casos particulares de la potenciación
- Cualquier potencia de exponente 0, es igual a 1 (siempre que su base no sea 0)
- Cualquier potencia de exponente 1, es igual a la base.
- Cero elevado a cualquier exponente (distinto de cero) es igual a cero.

Relación de orden entre las potenciaciones
Para establecer las relaciones de orden entre las potenciaciones procedemos de la siguiente manera:
- Si dos potencias son de igual base, la potencia mayor es la que tiene mayor exponente.
- Si dos potencias son de igual exponente, la potencia mayor es la que tiene mayor base.
- Todo número elevado a cero da como resultado uno.
- Todo número elevado a uno da como resultado el valor de la base.
Pulsa aquí para ampliar el contenido y ver como resolver los ejercicios.
Actividades
1. Representa las siguientes potencias
2. Convierte las siguientes multiplicaciones en potencias
San Diego, de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: División con números enteros decimales.
Dividir un número decimal entre un número entero
Se dividen como si fuesen enteros.
En la división al bajar el primer número decimal, se escribe la coma en el cociente.
Vamos a ver un ejemplo, dividiendo 77,5 entre 25
77 entre 25 es igual a 3.
3 x 5 = 15, al 7 van 2 y me llevo 1.
3 x 2 = 6 y una que me llevaba, son 7. Por lo tanto, al 7 son 0.
Ahora bajamos la siguiente cifra. Como el 5 es el primer número decimal, escribiremos la coma en el cociente. Y dividimos, 25 entre 25, que es igual a 1.
1 x 25 = 25, al 25 van 0.
El resultado de esta división de número decimal entre número entero es: 3,1 y el resto 0
Dividir un número entero entre un número decimal
Por ejemplo, vamos a dividir 278 entre 3,6
Debido a que no se puede hacer una división con un divisor decimal, lo primero que haremos es transformar nuestro divisor en un número entero (3,6 => 36). Para ello, hay que hacer dos cosas:
- Multiplicar el divisor por la unidad seguida de tantos ceros como cifras decimales queramos eliminar (3,6 x 10 = 36).
- Multiplicar el dividendo por el mismo número que hayamos multiplicado el divisor (278 x 10 = 2780).
Haciendo estas dos cosas lo que obtenemos es una división equivalente por la cual obtendremos el mismo cociente.
Por ejemplo, vamos a dividir 278 entre 3,6
Debido a que no se puede hacer una división con un divisor decimal, lo primero que haremos es transformar nuestro divisor en un número entero (3,6 => 36). Para ello, hay que hacer dos cosas:
- Multiplicar el divisor por la unidad seguida de tantos ceros como cifras decimales queramos eliminar (3,6 x 10 = 36).
- Multiplicar el dividendo por el mismo número que hayamos multiplicado el divisor (278 x 10 = 2780).
Haciendo estas dos cosas lo que obtenemos es una división equivalente por la cual obtendremos el mismo cociente.
7 x 3 = 21 y 4 que me llevaba son 25, al 27 son 2.
Ahora bajamos el 0, por lo que dividimos 260 entre 36, que es igual a 7.
7 x 6 = 42, al 50 van 8 y nos llevamos 5.
7 x 3 = 21 más 5 que nos llevábamos son 26, al 26 van 0.
El resultado de la división es 77 y de resto 8.
Debemos tener en cuenta que como hemos multiplicado el dividendo y el divisor por un mismo número (el 10 en este ejemplo), el cociente no sufre variación pero sin embargo el resto sí, ya que también ha quedado multiplicado por ese mismo número. Por tanto debemos dividir 8 entre 10 para obtener el resto de la división original (8:10 = 0,8).
Por tanto, quedaría una tercera cosa por hacer:
- Dividir el resto por el mismo número que hayamos multiplicado el divisor (8 : 10 = 0,8).
El resultado de esta división de número entero entre número decimal es 77 y resto 0,8.
Divisiones con números decimales en dividendo y divisor
Por ejemplo, vamos a dividir 278,1 entre 2,52
De nuevo debemos transformar nuestro divisor en un número entero, para ellos seguimos las mismas pautas que en el ejemplo anterior. En este caso hay dos decimales en el divisor, por lo que debemos multiplicarlo por 100 (2,52 x 100 = 252) y multiplicar por el mismo número el dividendo (278,1 x 100 = 27810)
De esta forma la división 278,1 : 2,52 se convertirá en 27810 : 252 después de multiplicar ambos números por 100.
Ahora dividimos 27810 entre 252.
278 entre 252 es igual a 1.
1 x 2 = 2, al 8 van 6.
1 x 5 = 5, al 7 van 2.
1 x 2 = 2, al 2 van 0.
Bajamos el siguiente número que es un 1, por lo que ahora tenemos que dividir 261 entre 252, que es 1.
1 x 2 = 2, al 11 van 9 y me llevo 1.
1 x 5 = 5, y 1 que me llevaba son 6, al 6 van 0.
1 x 2 = 2, al 2 van 0.
Bajamos el siguiente número que es un 0, por lo que ahora tenemos que dividir 90 entre 252. Como 90 es más pequeño que 252, tenemos que escribir 0 en el cociente y bajar la cifra siguiente. Como no hay más cifras, ya hemos terminado de realizar la división. Y el resultado sería 110 y de resto 90.
Pero como en el ejemplo anterior, el resto obtenido ha quedado multiplicado por el mismo número que dividendo y divisor y, para obtener el resto de nuestra división de origen, debemos dividirlo entre dicho número (90 : 100 = 0,9)
El resultado de esta división de número decimal entre número decimal es 110 y de resto 0,9
San Diego, 25 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Operaciones combinadas
Operaciones combinadas sin paréntesis
Para resolver estas operaciones sin paréntesis, se procede primero a efectuar las multiplicaciones o las divisiones, luego las adiciones o las sustracciones, en el orden en que aparecen.
Operaciones combinadas con paréntesis
Para las operaciones con paréntesis, se resuelve primero lo que está entre ellos y luego lo que están afuera, siguiendo el orden de las operaciones sin paréntesis.
San Diego, 12 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Ejercicios matemáticos
1) Aproximar las cantidades al orden indicado.
|
Número |
A
la Unidad de Mil |
A
la Centena |
A
la décima |
|
25 636,37 |
|
|
|
|
39 872,32 |
|
|
|
|
45 731,241 |
|
|
|
|
9 824,49 |
|
|
|
|
7 345,772 |
|
|
|
2)Ubicar las cantidades en la recta numérica.
-5,2; 8,3, -3,9; 7,1; -4,8; 3,5; -6,6; 4,2; 6,8; 2,8; -2,3; ,8,1
3) Establecer la relación de orden(≥) mayor que, (≤) menor que, e igual (=) a.
-8,3 ___ -4
-6,4 ___-6,9
3,3 ___ -9
-31,3 ___ 23,6
-16,2 ___1,16
-10___1
San Diego, 11 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Aproximación y Redondeo
Redondeo de números naturales y decimales Redondear un número natural o uno decimal es llevarlo al número más cercano terminado en cero. Por ejemplo, al redondear 47,2 m obtenemos como resultado 50 m.
Veamos otro ejemplo:

Aproximación de números decimales Aproximar un número decimal es llevarlo a la décima, centésima, milésima,... más cercana.Por ejemplo, la aproximación de 2,728 g a las centésimas es 2,73 porque 28 está más cerca 30 que de 20.
Veamos otro ejemplo:
San Diego, 08 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Los números negativos
Los números negativos son todos los números menores que el cero (0). Éstos números se expresan con el signo menos (-) a la izquierda de un número natural.
Los números negativos aparecen en muchas situaciones de nuestra vida diaria. cuando medimos temperaturas por debajo de cero grados, expresamos cantidades que adeudamos y las profundidades por debajo del nivel del mar.
Para leer un número negativo: se dice primero el signo (menos) y luego el número. Por ejemplo: -2 se lee: "menos dos".
Para escribir un número negativo: se escribe el menos (-) y el número. Por ejemplo: "menos siete" se escribe: -7.
Para ubicar los números negativos en la recta numérica:
- Se traza una recta y se divide en partes iguales.
- Debajo de la marca del centro se escribe el número cero.
- A la derecha del cero se escriben los números positivos, empezando por +1, y a la izquierda del cero, los negativos.

Relación de orden en los números negativos
Entre los números enteros negativos se pueden establecer las relaciones de orden (≥) mayor que, (≤) menor que, e igual (=) a.
- Entre dos números negativos, el mayor es el que tiene el menor parte entera o menor parte decimal. Ejemplo: -5,2 es mayor que -5,6. -3 es mayor que -4,3
-5,6 es menor que -5,2 -4,3 es menor que -3
- Entre un número negativo y un número positivo, el mayor siempre será el número positivo. Ejemplo: -3 es menor que 1,5 1,5 es mayor que -3
- Entre dos números positivos, el mayor es el que tiene mayor parte entera o parte decimal. Ejemplo: 1,5 es menor que 4,1 3 es mayor que -4,3
San Diego, 05 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Operaciones de multiplicación y división
Actividades de clase:
1) Ordena y multiplica:
a) 132,201 x 2,15=
b) 380,81 x 42,3=
c) 76421 x 7,10=
d 894,573 x 9,12=
e) 541,506 x 21,8=
2) Ordena y divide:
a) 5962,3 ÷ 21=
b) 201,341 ÷ 12=
c) 348256 ÷ 3,1=
d) 9648,73 ÷ 2,2=
e) 984,317 ÷ 8=
3) Escribe en letras las siguientes cantidades:
a) 2.450.316.500.702=
b) 761.000.420.005=
c) 960.456.231=
San Diego, 03 de Noviembre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Orden de los números naturales y números decimales
Un número decimal, por definición, es la expresión de un número no entero, que tiene una parte decimal. Es decir, que cada número decimal tiene una parte entera y una parte decimal que va separada por una coma, y son una manera particular de escribir las fracciones como resultado de un cociente inexacto. 
San Diego, 27 de octubre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Descomposición de números naturales y números decimales
Los números naturales y decimales se pueden descomponer en forma aditiva y de forma polinómica.
- Para descomponer 508 648 436 de forma aditiva se realiza de la siguiente forma:
- Para descomponer 508 648 436 de forma polinómica se realiza de la siguiente manera:
Veamos otros ejemplos:
Descomposición de 126 435 en forma aditiva y polinómica.
Los números naturales y decimales se pueden descomponer en forma aditiva y de forma polinómica.
- Para descomponer 508 648 436 de forma aditiva se realiza de la siguiente forma:
- Para descomponer 508 648 436 de forma polinómica se realiza de la siguiente manera:
San Diego, 25 de octubre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Sistemas de numeración quinario o base 5.
San Diego, 13 de octubre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Sistemas de numeración binario
En el sistema de numeración binario o base 2 se utiliza sólo dos símbolos (0,1) para expresar los números naturales.Para expresar el número 25 en sistema binario se divide el número y los sucesivos cocientes entre 2 hasta que el cociente sea menor que el divisor. Los residuos que den cero o uno de cada división se escribe de izquierda a derecha comenzando con el último cociente y terminando con el primer residuo. Observa el ejemplo:
San Diego, 06 de octubre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Sistemas de numeración posicional
Sistema de numeración decimal.
Utilizar diez cifras: 0,1,2,3,4,5,6,7,8,9
Tiene como base el número el número 10, es decir cada 10 unidades de un orden constituyen una unidad de orden inmediatamente superior.
El valor relativo de una cifra viene dado por el lugar que ocupa (unidades, decenas, centenas, etc).
San Diego, 04 de octubre de 2021
U. E. "Colegio Virgen de Coromoto"
6to grado
Mi nombre es:_________________________
Área: Matemáticas.
Tema: Sistemas de numeración No posicional
Los sistemas de numeración son conjuntos de símbolos que utilizamos para representar cantidades según ciertas reglas.
Sistema de numeración romano
Tiene siete símbolos representados por siete letras del abecedario latino:
La utilización de numeración romana está dotada de algunas reglas, que son necesarias recordar para poder formar números:
- Los símbolos V, L, D no se anteponen ni se repiten.
- Los símbolos I, X,C, M se pueden escribir hasta tres veces seguidas y sus valores se suman.
- El símbolo:
I se antepone únicamente a V y X
X se antepone únicamente a L y C
C se antepone únicamente a D y M
- Cualquier símbolo, escrito a la izquierda de otro de mayor valor, resta valor al de éste: IV= cuatro; XC= noventa.
- Cualquier símbolo, escrito a la derecha de otro mayor o igual, suma su valor al de éste: VI= seis; XX= veinte.
- Un trazo horizontal sobre los símbolos multiplica por 1000 el valor de todos ellos.























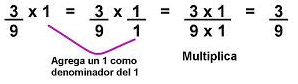


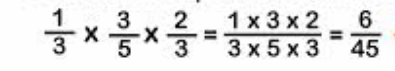
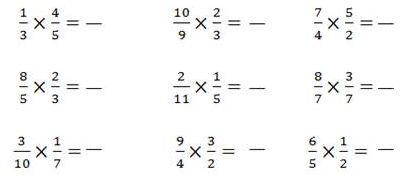














































No hay comentarios:
Publicar un comentario